A photon approached a semi-transparent mirror and asked “Will you let me pass through?”. The mirror kept silent for a minute and then replied “I don’t know. The god has not yet rolled the dice”.
Quantum mechanics is a theory that allows us to calculate the probabilities of random events happening in the nature at the very fundamental level. The emphasis here is on the words random and the probabilities. The word random tells us that the most basic events in the nature, like excitation of an atom or the reflection of a photon by a mirror, can not be predicted. In fact nature exhibits true randomness only in the quantum world. All other apparently random phenomenon is actually pseudo-random — governed by some complicated equation or a fancy algorithm. One exception to the last statement might be the randomness of our thought processes. But it is much safer not to ponder on this question.
So, if we can’t predict any fundamental event with certainty, what we do? We calculate the probabilities of the events we are interested in. This is what nature allows us to do, and quantum mechanics teaches us how to do.
Let’s take an example. Consider a photon incident on a beam-splitter . A beam-splitter is a device that splits a beam of light into a reflected part and a transmitted part. We may ask the question whether the photon incident on the beam-splitter will be reflected back or will be transmitted through. What comes next will amaze many. The answer to this question is that we don’t know. The nature does not have the answer to this stupidly simple question (or if it has, it has not yet told us).
In a sense it is almost sacred and frightening. On one hand nature has allowed us extraordinary scientific and technological feasts. It has allowed us to decode and play with the human genome. It has let us create new life forms. It has allowed us to hear the whispers of the merging of the black holes happened in a distant past. And it has brought us to the verge of the next big step in evolution in which we might be replaced by the machines we create. Yet it does not let us answer the simple question whether the photon will pass through the beam-splitter.
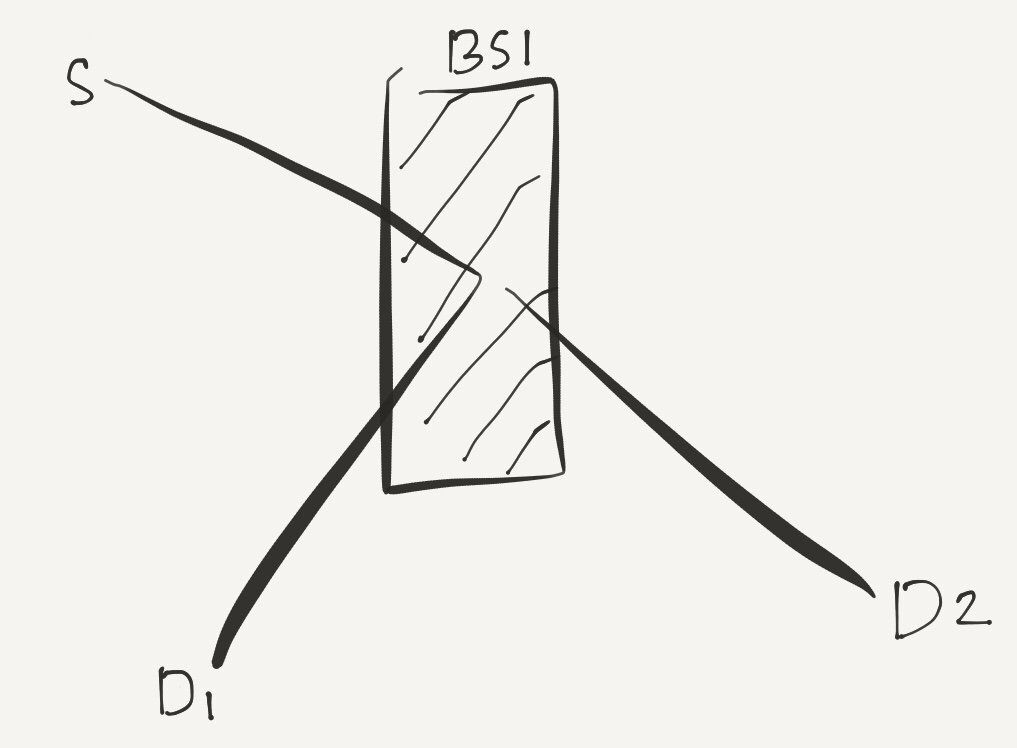
Coming back to our problem, if we run the experiment — striking a photon with the beam-splitter— a large number of times, we will find that the beam-splitter reflects the photon with the probability $latex r^2 $, and transmits it with the probability $latex t^2 $ with $latex r^2+t^2 =1 $. This is all we can tell about this simple experimental setup.
Let’s consider another experiment . In this one we introduce two mirrors and a second identical beam-splitter to the setup.
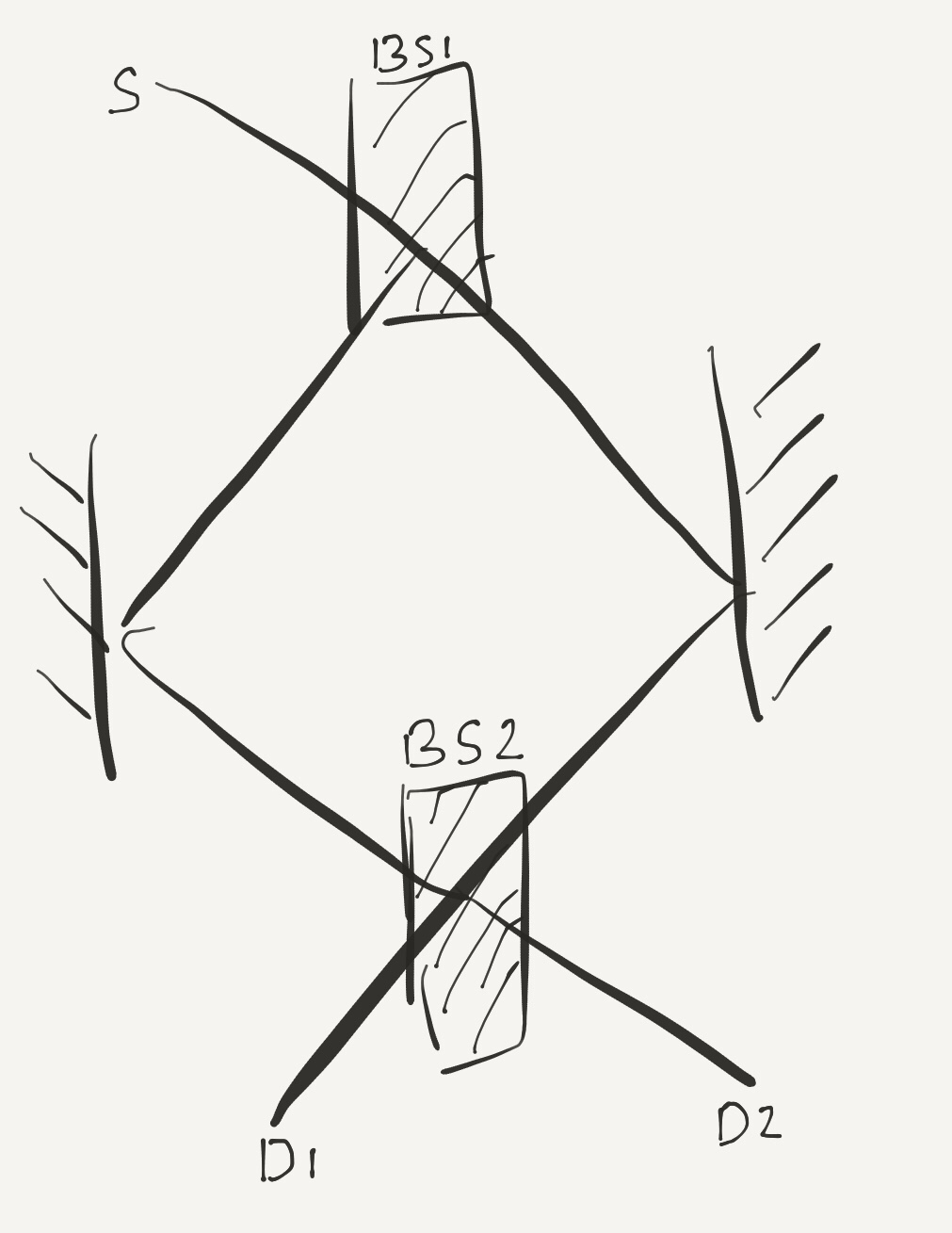
For this setup our intuition tells us that since both beam-splitters reflect and transmit the photon with the probabilities $latex r^2 $ and $latex t^2 $, respectively, the probability that the photon is detected at the detector D1 should be $latex r^4 + t^4$. And the probability that it is detected at D2 should be $latex 2r^2 t^2 $. However, this is not the case. If we perform the experiment a large number of times, we will see that a $latex (t^2-r^2)^2 $ fraction of all incident photons is detected at the detector D1, and $latex 4r^2t^2 $ fraction goes to the detector D2. We see here that for $latex r=t $, the detector D1 will never click. Moreover, we can see that by changing the relative path length along the two arms between the beam-splitters, we can change the probabilities of detection at the two detectors all the way from zero to one. This seems very much like an interference phenomenon in which by changing the path difference between the interfering paths we can get either the constructive or the destructive interference. Indeed it is the case in our present example.
In order to account for the experimental observations, and to understand the interference phenomenon discussed above we add this rule to our theory. If a quantum system can follow different paths, it will follow all those paths. To each path we can associate a complex amplitude which tells us how likely the quantum system is to follow that path. When different path reunite we add the corresponding amplitudes. Finally at the time of the measurement (for example the detection at detector D1), the modulus square of the complex amplitude gives the probability of detection. This is how quantum mechanics accounts for how nature behaves at the very fundamental level.
The setup shown in the last example is called the Mach-Zehnder interferometer. It holds some very deep mysteries of the nature. In the future posts we will try to appreciate some of these mysteries.
Leave a Reply