Position Operator: From Ket vectors to wavefunctions

Suppose we are interested in measuring the position of a quantum particle. The observable that will do the job is the position operator. The eigenvalue equation for position operator is

$latex \hat x \left|x\right\rangle=x \left|x\right\rangle&s=2$

Here $latex \left|x\right\rangle &s=2$ are position eigenkets and $latex x &s=2$ are the corresponding eigenvalues. This operator is different from the one we have already encountered for the energy and will need slightly different treatment. The eigenvalues of this operator are continuous. The completeness relation thus changes into an integration instead of a summation.

Completeness relation

We write the completeness relation for the eigenkets of position operator as

$latex \int_{-\infty}^{\infty}dx \left|x\right\rangle\left\langle x\right|=\hat I&s=2$

We can use this completeness relation to write any arbitrary ket as

$latex \left|\psi\right\rangle=\hat I \left|\psi\right\rangle=\int_{-\infty}^{\infty}dx \left|x\right\rangle\left\langle x|\psi\right\rangle &s=2$

Wavefunctions and probability density

The scalar product/expansion coefficient/probablity amplitude  $latex \left\langle x|\psi\right\rangle &s=2$ is called (position space) wavefunction.  We write it as

$latex \psi(x)=\left\langle x|\psi\right\rangle &s=2$

Wavefunctions are the scalar product of ket vectors with position eigenkets.

The modulus square of the wave function is again related to the probability of the measurement outcome of the position meaurement of the particle. However due to the continuous nature of the eigenvalues of this operator, we need to modify the corresponding postulate (Postulate 4 discussed in the class). The postulate that gives the probabilities of measurement outcome of position measurement of the quantum particle can be stated as follows:

The probability of obtaining the position of the particle in a narrow strip of width $latex dx &s=2$ centered at $latex x=x_0 &s=2$ is given by $latex |\psi(x_0)|^2dx &s=2$

This can be seen in the figure below

 

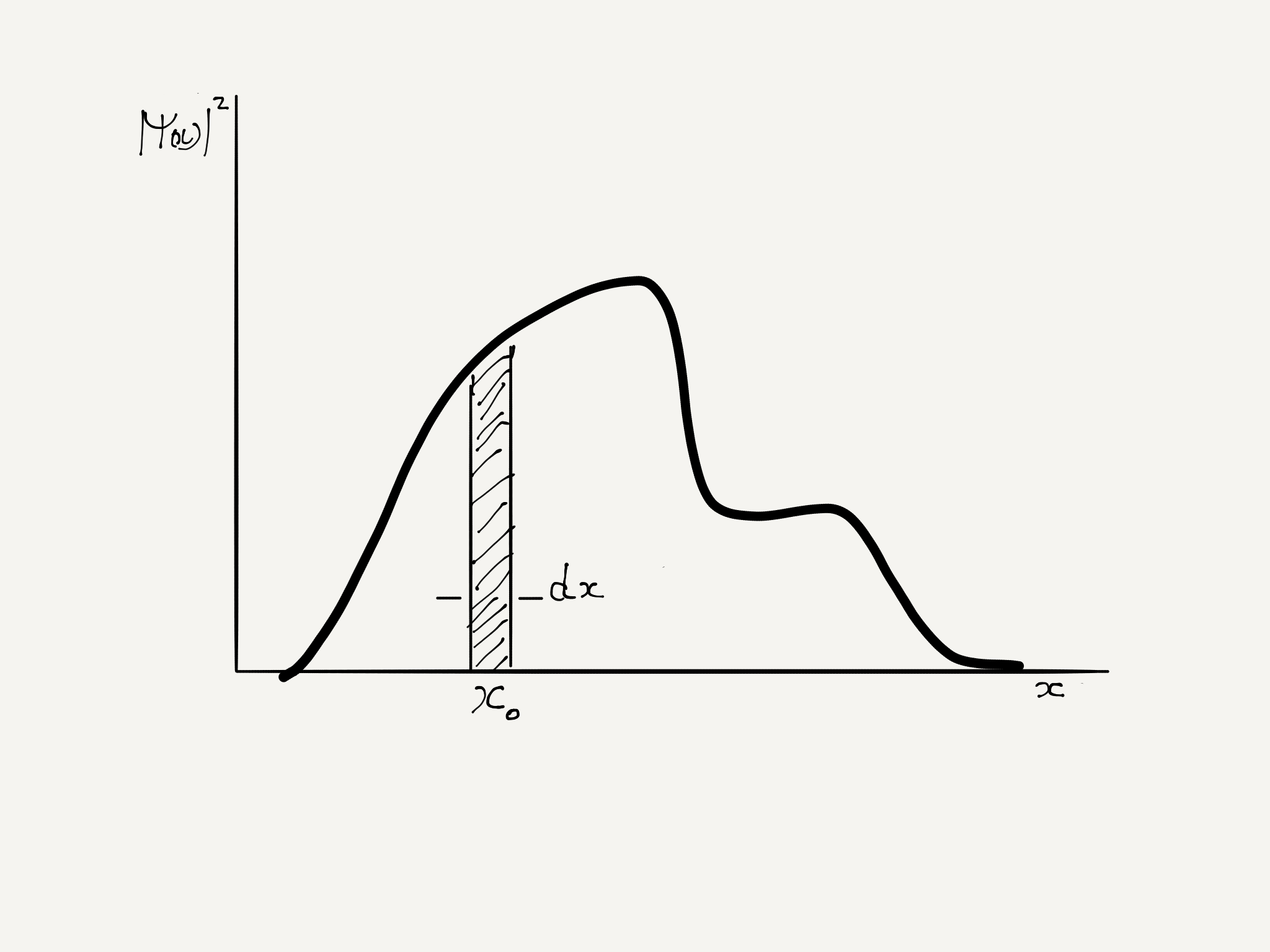
The quantity plotted as the function of $latex x&s=2$ is  $latex |\psi(x)|^2&s=2$ and is called probability density. Obviously the probability of finding a particle in a location is higher if the probability density is high over there. We can now also answer the questions like “What is the probability of finding the particle between $latex x=a&s=2$ and $latex x=b&s=2$. This probability will be $latex \int_a^b|\psi(x)|^2dx&s=2$.

Scalar product as an integral

Another use of the completeness relation is to write the scalar product in the form of an integral. Consider the norm of the vector $latex \left|\psi\right\rangle&s=2$

$latex \left\langle\psi|\psi\right\rangle=\left\langle\psi|\hat I|\psi\right\rangle=\int_{-\infty}^{\infty}\left\langle\psi|x\right\rangle\left\langle x|\psi\right\rangle dx=\int_{-\infty}^{\infty} \psi^*(x)\psi(x) dx=1&s=2$

More generally the scalar product of two vectors can be written as

$latex \left\langle\phi|\psi\right\rangle=\left\langle\phi|\hat I|\psi\right\rangle=\int_{-\infty}^{\infty}\left\langle\phi|x\right\rangle\left\langle x|\psi\right\rangle dx=\int_{-\infty}^{\infty} \phi^*(x)\psi(x) dx&s=2$

Orthogonality relation

The orthogonality condition is also modified in case of continuous spectrum. It is given as follows for the position eigenkets

$latex \left\langle x^\prime|x\right\rangle=\delta(x^\prime-x)&s=2$

The expression on right is called Dirac delta function. Its value is zero if the argument is non-zero. If the argument is zero then the value of the function is undefined. However the integration over this undefined value is unity. We write it

$latex \int \delta(x)=1&s=2$.