Nature speaks linear algebra

In our previous post we considered a simple interferometric  experiment and claimed that quantum mechanics can account for the experimentally observed detection probabilities in the interferometer. In this post we will see how it is done. The idea was to to attach complex amplitudes to all paths available to the photon. Mathematically it can be done by borrowing tools from linear algebra, and describing  the state of the photon in terms of vectors— which can be conveniently represented as matrices. This brings us to the very first lesson.This is test $latex \hbar=2$

The states of a quantum system are described by vectors

Let’s again consider the simple Mach-Zehnder interferometer.

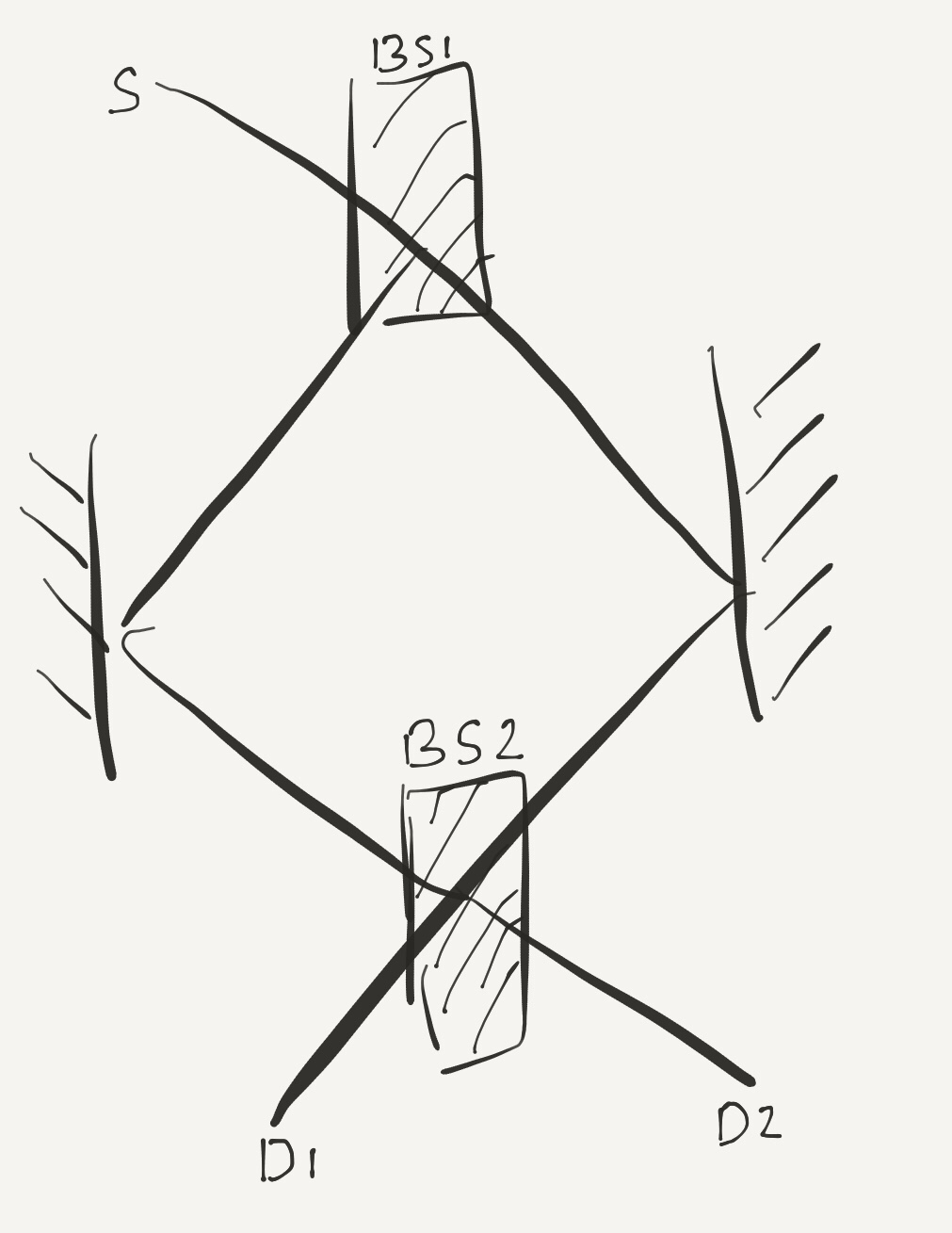
We can identify two paths between the source S, and the detectors D1 and D2. Let’s represent these as follows

• The  matrix $latex \begin{pmatrix} 1 \\  0\end{pmatrix}$ represents the state in which the photon is on the left side of the two beam-splitters. We can note that initially when the photon is emitted from the source, it is in state $latex \begin{pmatrix} 1 \\ 0\end{pmatrix}$.
• The  matrix $latex \begin{pmatrix} 0 \\ 1\end{pmatrix}$ represents the state in which the photon is on the right side of the beam-splitters.

The photon in the state $latex \begin{pmatrix} 1\\0 \end{pmatrix}$ approaches the first beam-splitter. The beam-splitter splits the state of the photon in two parts. Please note here  that the splitting takes place for the state which is a vector, and not for the photon which is a physical entity.

The splitting takes place for the state which is a vector, and not for the photon which is a physical entity.

Mathematically the beam-splitter action can be represented as follows

$latex \begin{pmatrix} ir & t \\ t & ir \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} =ir \begin{pmatrix} 1 \\ 0 \end{pmatrix} +t \begin{pmatrix} 0 \\ 1\end{pmatrix} &s=2 $

The first 2×2 matrix in the above equation represents the action of the beam-splitter.

The next coulumn matrix is the initial state of the photon. The right side of the equation is the state of the photon after passing through the first beam-splitter.

Here we see that the moudulus square of the complex amplitudes assoicated with the two paths give us the correct reflection and transmission probabiliteies $latex r^2$ and $latex t^2$, respectively.

Also note that $latex i =\sqrt{-1}$ is the phase difference between the reflected and transmitted amplitudes. It comes from the requirement of unitarity of beam-splitter transformation— a concept that we will learn in another post.

After the first beam-splitter we have two mirrors which do not change the state of the photon. Finally, the photon approaches the second beam-splitter in the state $latex \begin{pmatrix} ir \\ t \end {pmatrix}$. The action of the second beam-splitter is given by

$latex \begin{pmatrix} ir & t \\ t & ir \end{pmatrix} \begin{pmatrix} ir \ \ t \end{pmatrix} =(-r^2+t^2 )\begin{pmatrix} 1 \\ 0 \end{pmatrix} +2 irt \begin{pmatrix} 0\\ 1 \end{pmatrix} &s=2$

The right hand side of the above equation yields the state of the photon after the second beam-splitter. The modulus square of the amplitudes
$latex (t^2-r^2)^2$ and  $latex 4r^2t^2$ correctly give the experimentally verifiable detection probabailities of D1 and D2 detectors, respectively.

Summary

Here is a quick review of what we have learned so far

• The state of a quantum system is described by a vector which can be represented as  a coulumn matrix. We will later see that we can also represent the states as row matrices, or using analytic  functions.
• The operations on quantum systems are carried out by operators that can be represented as square matrices.
• The modulus  square of the complex amplitudes are related to experimentally observed probabilities.